Probabilistic Graphical Modeling / Network Data Analysis
Predicting confirmed cases of various epidemics using global temporal-feature-based graph convolutional network
Objective
The prediction of infectious disease spread is a challenging task as it is influenced by various factors. In this paper, we propose the GLObal temporal feature-based Graph Convolutional Network (GLOGCN), which focuses on the global temporal patterns present in the spread of infectious diseases. Epidemic datasets may contain anomalous data, but by leveraging global temporal patterns, the model can effectively capture the overall trends of disease propagation.
Data
The COVID-19 Data Repository by the Center for Systems Science and Engineering at Johns Hopkins University, the Hungarian chickenpox [1], and The German tuberculosis [2] datasets are employed to validate GLOGCN.
[1] B. Rozemberczki et al., “Chickenpox cases in hungary: a benchmark dataset for spatiotemporal signal processing with graph neural networks”, 2021.
[2] SurvStat@RKI 2.0. Robert koch institute, 2023.
.
Related Work
The input of graph-based models is both temporal data and spatial data, which are the newly confirmed cases of the epidemic and a geographical-based adjacency matrix, respectively.
Spatio-Temporal Graph Convolution Network (STGCN) [3] is a typical graph model for dealing with time series. it handles the local temporal features using temporal gated convolution and processes the spatial information through spatial graph convolution.
EpiGNN [4] is a graph neural network-based model for epidemic forecasting. it employs transmission risk encoding, which characterizes the spatial effects of each region. The multi-scale convolution captures the local temporal features and the GCN investigates the spatial information with the temporal features.
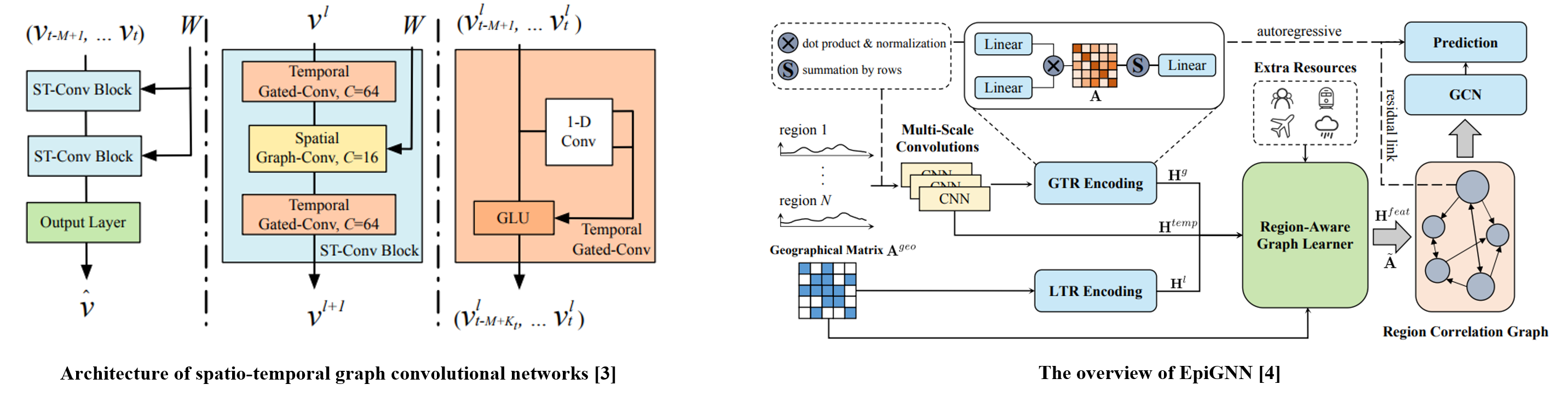
[4] F. Xie et al., “EpiGNN: Exploring spatial transmission with graph neural network for regional epidemic forecasting”, 2022.
Proposed Method
The proposed model takes the past new confirmed cases of the epidemic in every region as an input given a geographical-based adjacency matrix. The model forecasts the future new confirmed cases of the epidemic for every region.
First, the global temporal feature extractor (GTFE) processes an input to produce the global temporal features and dynamic adjacency matrix. The integration block comprises data-processing of temporal gated convolution (TGC), self-attention layer, and spatial graph convolution and involves fusing global temporal features from GTFE. The output block, consisting of several feedforward networks, projects the spatio-temporal latent features into the prediction of future new confirmed cases.
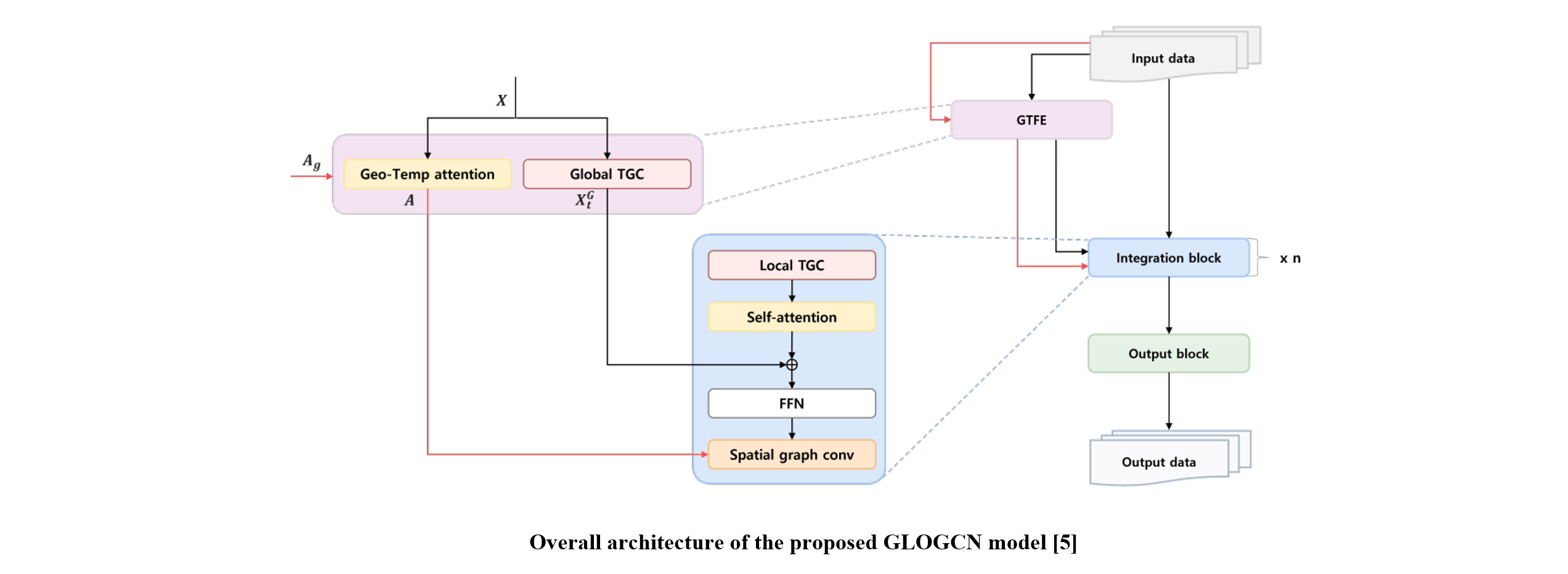
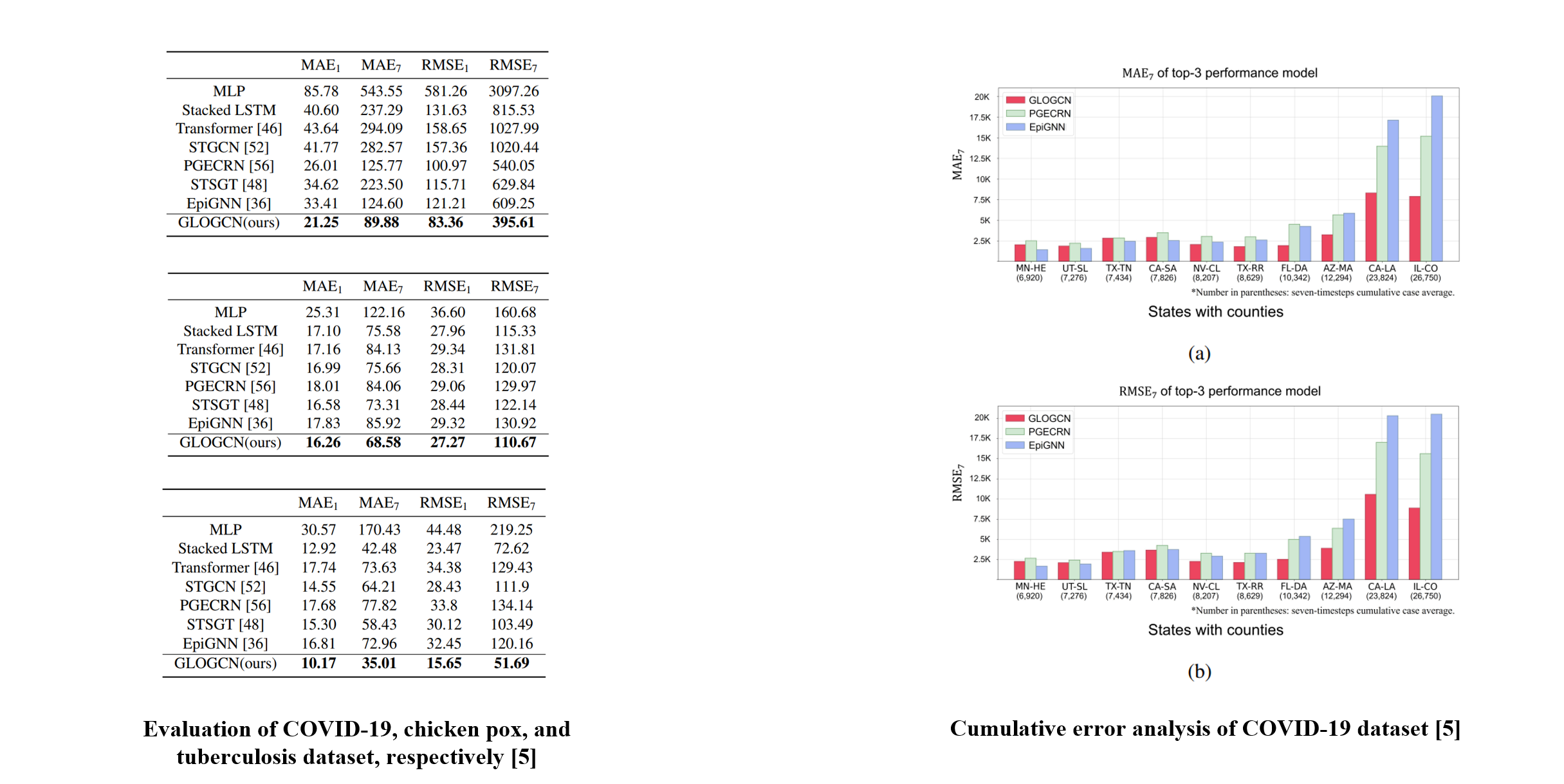
The experimental results on each dataset evaluation suggested that the proposed GLOGCN achieves the lowest error on predicting the future new confirmed cases of the epidemic.
In addition, GLOGCN exhibited outstanding performance even in regions with a high number of new confirmed cases.
It is noteworthy that most model parameter numbers tended to increase excessively depending on the number of regions. However, the increase in the gap of the parameters of GLOGCN was small considering its high performance.
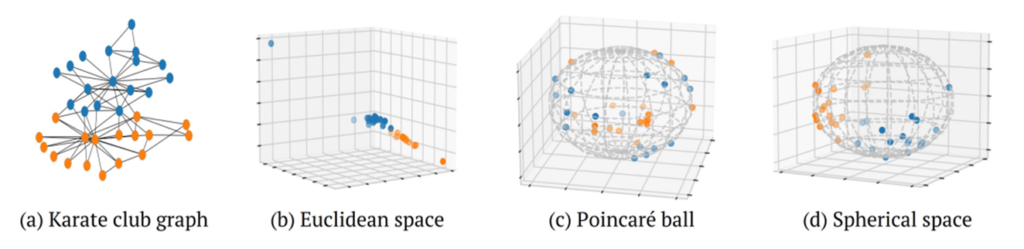
Data is mainly represented in Euclidean space for a variety of reasons. One of the main reasons is that Euclidean space is more intuitive than other spaces. Linear algebra and vector structures were also researched based on Euclidean space. As a result, the forms of the distance and inner product, the tools of measurement we commonly use, are mostly defined in Euclidean space. Due to this strong familiarity associated with Euclidean space, Euclidean geometry research has been active in machine learning.
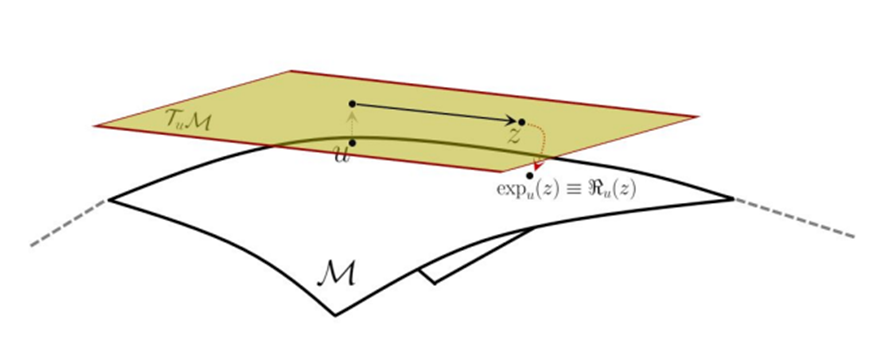
A hyperbolic space of dimensions is a complex structure compared to Euclidean space. Therefore, in order to solve the optimization problem through a simpler approach, we suggest the use of a sphere, referred to as Poincaré ball. The Poincaré ball is a conformal structure of hyperbolic space. As in the case of the sphere, we can use a first-order approximation of the exponential map, called a retraction.
The unit sphere is selected primarily when applying optimization problems in the spherical space. Similar to the Poincaré ball, the unit sphere can apply a first-order approximation method to use retraction instead of the exponential map.
Artificial Intelligence Research for Monomer Design
[2021-08-01 ~ 2023-07-31, Samyang]Research Goal: to develop an artificial intelligence technology to design polymer with desired properties and create a structure-property database.
(1) Created a property database by collecting polymer data from public databases and literature.
- Analyzed properties of each database and developed an auto-collecting tool for easy and fast collection. The auto-collecting tool can collect data that is updated later.
(2) Developed an artificial intelligence technology to analyze the relationship between molecule structures and properties.
- Developed a new line notation for organic compounds and created a dataset that is required to train the artificial intelligence model.

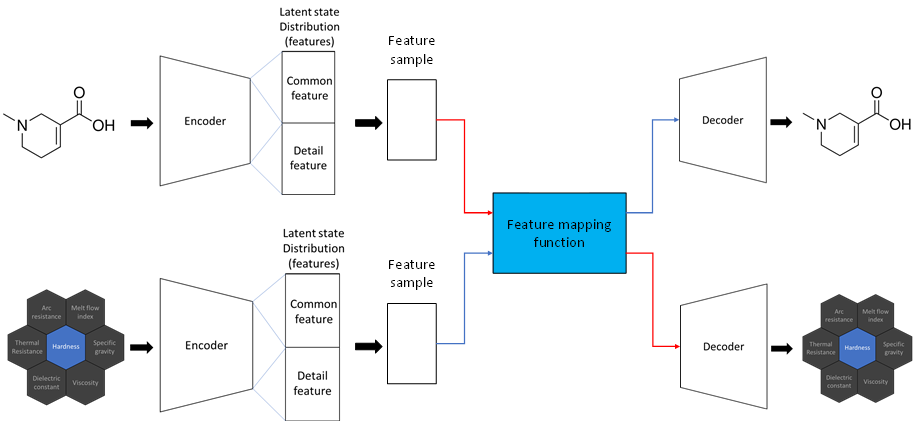
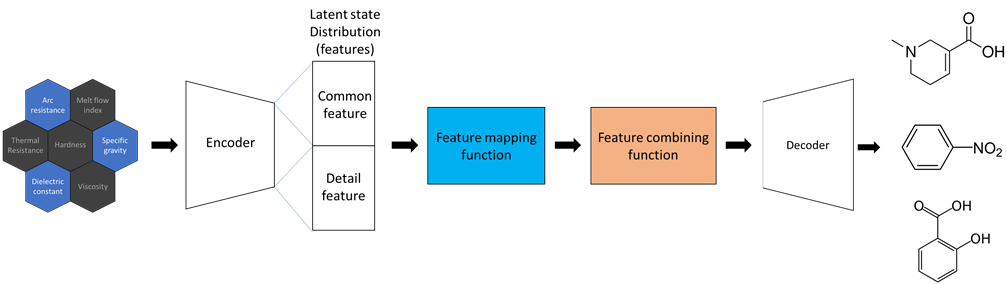
(3) Explored the latent space to find a relationship between molecule structures and properties.
- Exploring latent space that represents correlations within properties allows property analysis with low computational costs.
- Attempted to apply VAE (Variational Auto Encoder)
(4) Generative Model-based Structure Prediction
- Developed an artificial intelligence technology that predicts molecule structures with desired properties.
Graph Embedding in Non-Euclidean Space
Objective
Depending on the domain of the data, there are different appropriate metrics, such as the Euclidean distance, the cosine similarity, and the geodesic distance. In other words, it is not necessary for the embedding space to be Euclidean space. Despite the fact that data from various areas are represented as graph-structured data, non-Euclidean space is not effortlessly considered as a common embedding space in graph embedding.
Data
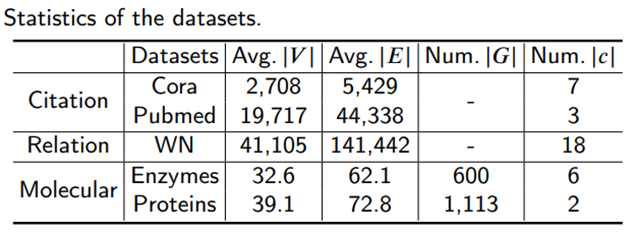
We compare the reciprocal with each space on our experimental benchmark, including citation, molecule, and relation networks.
Related Work
Dobson, D.P., Doig, J.A., 2003. Distinguishing enzyme structures from non-enzymes without alignments. Journal of Molecular Biology , 771–783.
Namata, G., London, B., Getoor, L., Huang, B., 2012. Query-driven active surveying for collective classification, in: ICML Workshop on MLG.
McCallum, A., Nigam, K., Rennie, J., Seymore, K., 2000. Automating the construction of internet portals with machine learning. Inf. Retr. 3, 127–163. URL: https://doi.org/10.1023/A:1009953814988, doi:10.1023/A:1009953814988.
Borgwardt, K.M., Kriegel, H.P., 2005b. Shortest-path kernels on graphs, in: Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM 2005), IEEE Computer Society, Washington, DC, USA. pp. 74–81. URL: http://dx.doi.org/10.1109/ICDM.2005. 132.
Proposed Method
We generalize graph embedding in a certain space at the graph-level as well as at the node-level. Also, we compare the reciprocals with each space on the benchmark commonly used and suggest directions by which to determine the embedding space when confronted with certain types of data. From the experimental results, we contend that graph-level embedding in non-Euclidean space is superior to embedding in Euclidean space.
Latent graph structure pooling with a hierarchical graph context representation.
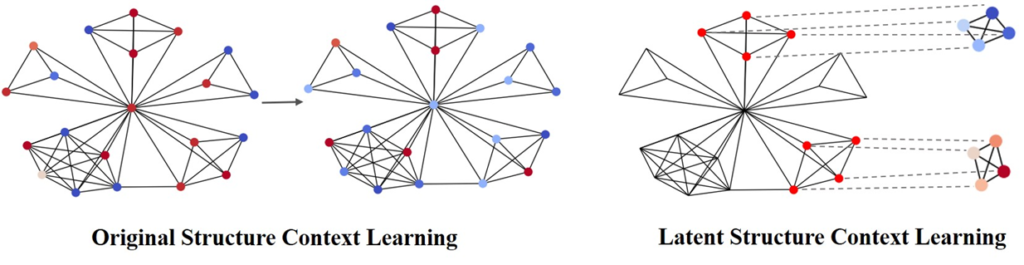
In graph data analysis, particularly the graph classification task, a discriminative graph-level representation is significant to improve classification performance. For the performance improvement, recent studies have applied pooling methods to graph neural networks.
However, the existing pooling approaches lose the initial graph structural information when incorporating each node. When a latent structure obtained from the pooling operation is given, the nodes in each latent structure have a different significance compared with the original graph. This structural information discrepancy between initial and latent structures leads to an inadequate graph representation when the existing methods generate the graph result. Motivated by this, we study propose a latent graph structure pooling with a hierarchical graph context representation.
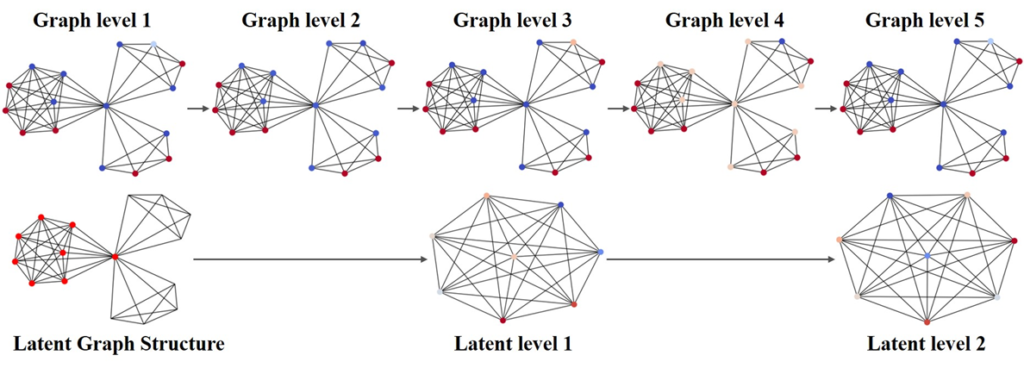
The context attention module emphasized relatively significant nodes in the given graph. The original graph was sampled from the IMDB-BINARY dataset, and the latent structure was extracted from the original graph. Following the visualization result, a contextual difference was observed between the original graph and latent structure. In the original graph level, a few nodes were represented as commonly significant and fixed in each context block. In contrast, the latent level was highly focused on the two nodes in the latent context. Even though the latent structure had the same connections as the original, it emphasized different contextual information.
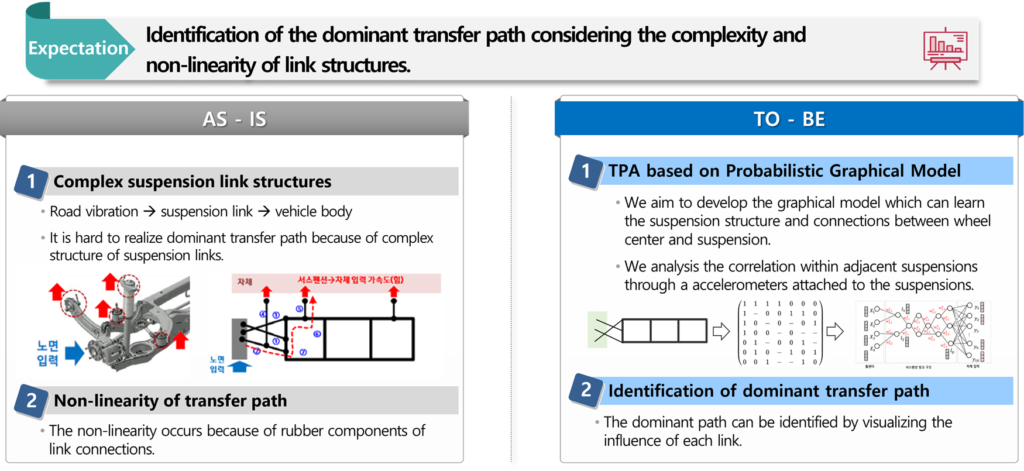
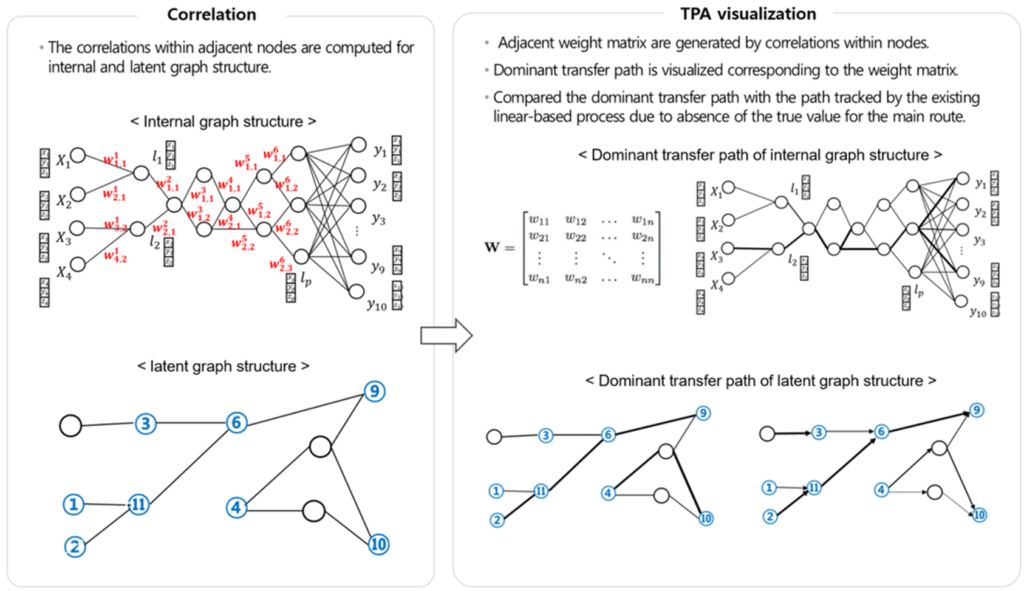
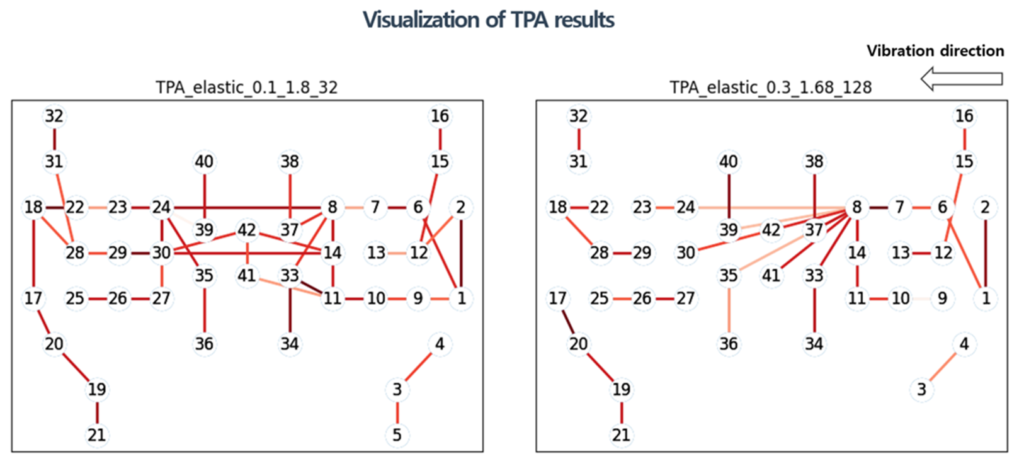
Developed an analysis model that can be applied to complex link structures through Transfer Path Analysis(TPA) in suspension link units.